ホーム / 05. 特性方程式と固有値 /

はじめに

状態方程式から離散化した逐次式へ で求めた離散化した逐次式

\[x(t+Δt)=Px(t)+Qu(t)\]\[P=I+AΔt(I-\frac{Δt}{2}A)^{-1}\]\[Q=Δt(I-\frac{Δt}{2}A)^{-1}B\]

を用いてバネマスモデルの時間応答の確認（シミュレーション）をしていきます。

バネマスモデル

状態方程式によるモデル化でバネマスモデルの状態方程式を導出しました。システムの入力として、質量𝑀の荷重に加え外部から荷重𝛥𝑀が加わるものとしています。

\[\frac{d}{d t}\left[\begin{array}{l}x \\\dot{x}\end{array}\right]=\left[\begin{array}{cc}0 & 1 \\-\frac{K}{M} & -\frac{D}{M}\end{array}\right]\left[\begin{array}{l}x \\\dot{x}\end{array}\right]+\left[\begin{array}{c}0 \\\frac{g}{M}\end{array}\right](M+\Delta M)\]

状態方程式を離散化した逐次式に変換

バネマスモデルの状態方程式を逐次式に変換します。

こちらからExcelファイルをダウンロードできます。

Excelの状態方程式のシートでは下記のように行列の積の関数MMULTや逆行列の関数MINVERSEを使うことで、離散化した逐次式のPとQを計算しています。逐次式にすることによりExcelでのシミュレーションが容易になります。

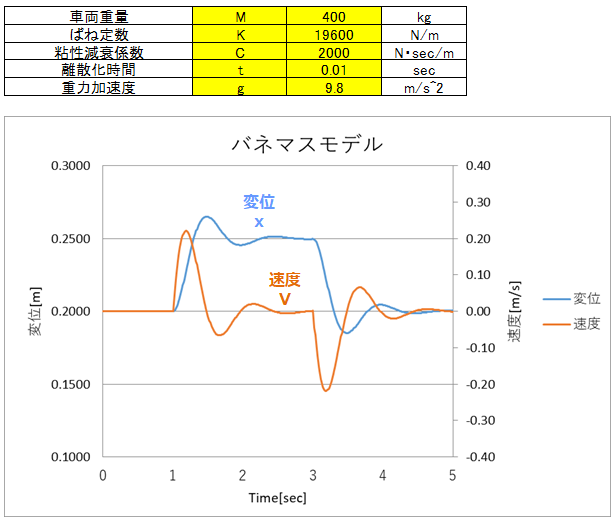
時間応答の確認

Excelのシミュレーションのシートでは、状態方程式のシートで計算した逐次式のPとQを使い、逐次式\[x(t+Δt)=Px(t)+Qu(t)\]によって時間応答を計算しています。Excelの1行が離散時間Δtです。

行列演算をEXCELシート上に展開

加重 M+ΔM、変位 𝑥、変位速度 𝑣 とP, Q を行列演算しています。逐次Δt後の変位 𝑥 と変位速度 𝑣 を算出し、結果をEXCELシート上に展開することで時間応答を求めています。


上部のスライドボリュームでばね定数やダンパーの粘性減衰係数、入力荷重を変更することにより時間応答の変化を確認することができます。シミュレーションによりシステムの挙動におけるばね定数や粘性減衰係数の影響を把握できます。

下のグラフは時間1秒から3秒の間に外部から200kgの入力荷重が加わった場合の挙動を示しています。

システムの安定性分析　～固有値

状態方程式からシステムの固有値を求めれば安定性を分析することができます。
特性方程式の解である固有値 λ は、状態方程式の行列Aを用いて以下のように求めます。

システムの状態方程式

\[\frac{d}{d t}\left[\begin{array}{l}x \\\dot{x}\end{array}\right]=\left[\begin{array}{cc}0 & 1 \\-\frac{K}{M} & -\frac{D}{M}\end{array}\right]\left[\begin{array}{l}x \\\dot{x}\end{array}\right]+\left[\begin{array}{c}0 \\\frac{g}{M}\end{array}\right](M+\Delta M)\]

特性方程式

\[ \operatorname{det}(\lambda I-A)= \operatorname{det}\left(\lambda I-\left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right]\right)\\ \] \[ =\operatorname{det}\left(\left[\begin{array}{cc} \lambda & -1 \\ \frac{K}{M} & \lambda+\frac{D}{M} \end{array}\right]\right)=\lambda^{2}+\frac{D}{M} \lambda+\frac{K}{M} \\ \]

固有値 λ（特性方程式の解）は2次式の解の公式から

\[ \lambda=-\frac{D}{2 M} \pm \frac{1}{2} \sqrt{\frac{D^{2}}{M^{2}}-\frac{4 K}{M}} \]

固有値 λ の実数部と虚数部を複素平面にマッピング

Excelのシミュレーションのシートに固有値 λ の実数部と虚数部を複素平面にマッピングしたグラフを作っています。

上部のスライドボリュームでばね定数やダンパーの粘性減衰係数を変更することにより固有値 λ によるシステムの挙動の変化を確認することができます。

  • 粘性減衰係数を0[N・sec/m]に変更すると
    → 固有値の実部が負でなくなり、収束しなくなる。

  • 粘性減衰係数を増加させると振動的な挙動はなくなる。
    ばね定数19600[N/m]、粘性減衰係数5600[N・sec/m]では、固有値の虚数部もなくなり、さらに収束性が向上する。

  • 離散時間系の固有値は絶対値＜１で安定する。

システムの安定条件

システムの安定条件をまとめると以下になります。

　システムの安定性は特性方程式の解（固有値）から分析でき、

　　連続時間系：固有値の実部が負
　　離散時間系：固有値の絶対値＜１

システムの安定性の条件は、現代制御（オブザーバ、状態フィードバック）のゲイン設定にも利用します。

最後までお読みいただき、ありがとうございました。

この後は、システムの同定、フィードバック制御、フィードフォワード制御、非線形なシステムへの対応と続きますが、ここまで説明した高精度な離散時間モデルの作り方とシステムの安定性の条件の知見があれば、現代制御（オブザーバ、状態フィードバック）に進むこともできます。


QooQ